Pythagorasatsningen säger att summan av kvadraterna på benen i en höger triangel är lika med kvadraten på hypotenusen (sidan motsatt rät vinkel) - i välbekant algebraisk notation, a 2 + b 2 = c 2. Babylonierna och egyptierna hade hittat några heltal tredubblar ( a , b , c ) som tillfredsställde förhållandet. Pythagoras (cirka 580 - cirka 500 f.Kr.) eller en av hans anhängare kan ha varit den första som bevisade satsen som bär hans namn. Euclid (ca 300 f.Kr.) erbjöd en smart demonstration av Pythagoras teorem i sina element , känd som väderkvarnsäker från figurens form.
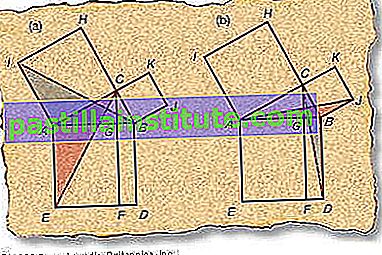
- Rita kvadrater på sidorna av den högra Δ A B C .
- B C H och A C K är raka linjer eftersom ∠ A C B = 90 °.
- ∠ E A B = ∠ C A I = 90 °, enligt konstruktion.
- ∠ B A I = ∠ B A C + ∠ C A I = ∠ B A C + ∠ E A B = ∠ E A C , med 3.
- A C = A I och A B = A E , enligt konstruktion.
- Därför Δ B A I ≅ Δ E A C , vid sidan av vinkel-sida-satsen (se sidofält: The Asses Bridge), som markeras i figur (del).
- Dra C F parallellt med B D .
- Rektangel A G F E = 2Δ A C E . Detta anmärkningsvärda resultat härrör från två preliminära satser: (a) områdena för alla trianglar på samma bas, vars tredje topp ligger var som helst på en obestämd förlängd linje parallell med basen, är lika; och (b) ytan av en triangel är hälften av varje parallellogram (inklusive vilken rektangel som helst) med samma bas och höjd.
- Kvadrat A I H C = 2Δ B A I , med samma parallellogramsats som i steg 8.
- Därför rektangel A G F E = kvadrat A I H C , steg 6, 8 och 9.
- ∠ D B C = ∠ A B J , som i steg 3 och 4.
- B C = B J och B D = A B , genom konstruktion som i steg 5.
- Δ C B D ≅ Δ J B A , som i steg 6 och markerad i del (b) i figuren.
- Rektangel B D F G = 2Δ C B D , som i steg 8.
- Kvadrat C K J B = 2Δ J B A , som i steg 9.
- Därför rektangel B D F G = kvadrat C K J B , som i steg 10.
- Kvadrat A B D E = rektangel A G F E + rektangel B D F G , efter konstruktion.
- Därför är kvadrat A B D E = kvadrat A I H C + kvadrat C K J B , steg 10 och 16.
Den första boken med Euclids elementbörjar med definitionen av en punkt och slutar med den pythagoreiska satsen och dess konversation (om summan av kvadraterna på två sidor av en triangel är lika med kvadraten på den tredje sidan måste den vara en rätt triangel). Denna resa från en specifik definition till ett abstrakt och universellt matematiskt uttalande har ansetts vara symboliskt för utvecklingen av det civiliserade livet. Ett slående exempel på identifieringen av Euklids resonemang med det högsta tanketrycket var förslaget från en tysk fysiker och astronom 1821 att inleda en konversation med Mars invånare genom att visa dem våra anspråk på intellektuell mognad. Allt vi behövde göra för att locka deras intresse och godkännande, hävdades det, var att plöja och plantera stora åkrar i form av väderkvarnsdiagrammet eller, som andra föreslog,att gräva kanaler som tyder på Pythagoras sats i Sibirien eller Sahara, fylla dem med olja, sätta dem i brand och vänta på svar. Experimentet har inte prövats och lämnar osäker om invånarna i Mars inte har något teleskop, ingen geometri eller ingen existens.








